Pgls Between Discrete and Continuous Variables
In this exercise we will learn how to do analyses using PGLS.
First, we will need a few libraries installed.
library ( ape ) library ( geiger ) library ( nlme ) library ( phytools ) ## Loading required package: maps ## Loading required package: rgl ## Warning: failed to assign RegisteredNativeSymbol for getData to getData ## since getData is already defined in the 'phangorn' namespace setwd ( "~/Documents/teaching/revellClass/2014bogota" ) Second, we will need some data. We can read in anolis data and a phylogenetic tree. You can download the files from the following addresses:
anolisDataAppended.csv
anolis.phy
Download these files and place them in your working directory.
anoleData <- read.csv ( "anolisDataAppended.csv" , row.names = 1 ) anoleTree <- read.tree ( "anolis.phy" ) Let's see what this tree looks like.
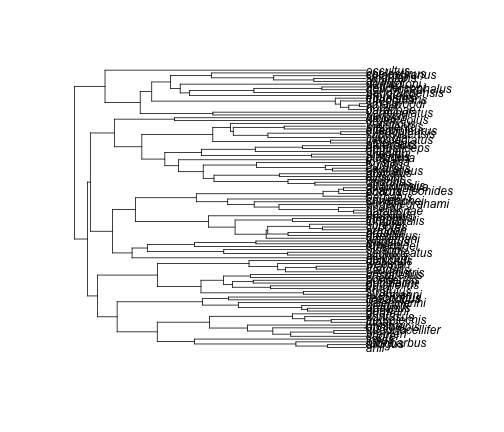
Geiger has a function to check that the names match between the tree and the data frame.
name.check ( anoleTree , anoleData ) Is there a correlation between awesomeness and hostility?
plot ( anoleData [, c ( "awesomeness" , "hostility" )]) 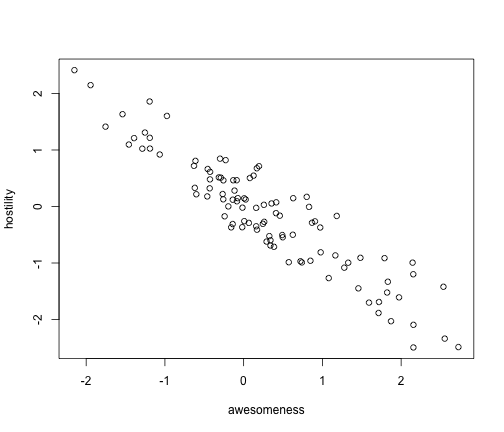
It certainly looks like there is. We can do this analysis easily with PICs, as you just learned:
# Extract columns host <- anoleData [, "hostility" ] awe <- anoleData [, "awesomeness" ] # Give them names names ( host ) <- names ( awe ) <- rownames ( anoleData ) # Calculate PICs hPic <- pic ( host , anoleTree ) aPic <- pic ( awe , anoleTree ) # Make a model picModel <- lm ( hPic ~ aPic - 1 ) # Yes, significant summary ( picModel ) ## ## Call: ## lm(formula = hPic ~ aPic - 1) ## ## Residuals: ## Min 1Q Median 3Q Max ## -2.105 -0.419 0.010 0.314 4.999 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## aPic -0.9776 0.0452 -21.6 <2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.897 on 98 degrees of freedom ## Multiple R-squared: 0.827, Adjusted R-squared: 0.825 ## F-statistic: 469 on 1 and 98 DF, p-value: <2e-16 # plot results plot ( hPic ~ aPic ) abline ( a = 0 , b = coef ( picModel )) 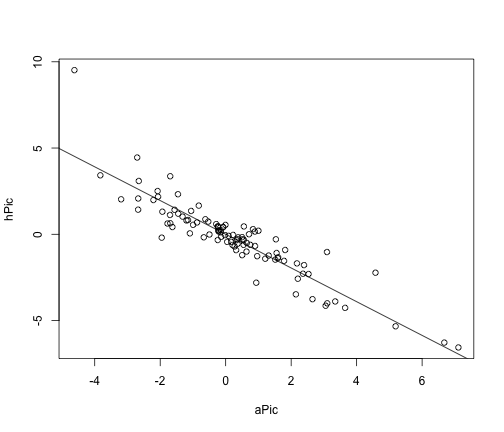
This whole procedure can be carried out more simply using PGLS.
pglsModel <- gls ( hostility ~ awesomeness , correlation = corBrownian ( phy = anoleTree ), data = anoleData , method = "ML" ) summary ( pglsModel ) ## Generalized least squares fit by maximum likelihood ## Model: hostility ~ awesomeness ## Data: anoleData ## AIC BIC logLik ## 191 198.8 -92.49 ## ## Correlation Structure: corBrownian ## Formula: ~1 ## Parameter estimate(s): ## numeric(0) ## ## Coefficients: ## Value Std.Error t-value p-value ## (Intercept) 0.1506 0.26263 0.573 0.5678 ## awesomeness -0.9776 0.04516 -21.648 0.0000 ## ## Correlation: ## (Intr) ## awesomeness -0.042 ## ## Standardized residuals: ## Min Q1 Med Q3 Max ## -0.76020 -0.39057 -0.04942 0.19597 1.07374 ## ## Residual standard error: 0.8877 ## Degrees of freedom: 100 total; 98 residual ## (Intercept) awesomeness ## 0.1506 -0.9776 plot ( host ~ awe ) abline ( a = coef ( pglsModel )[ 1 ], b = coef ( pglsModel )[ 2 ]) 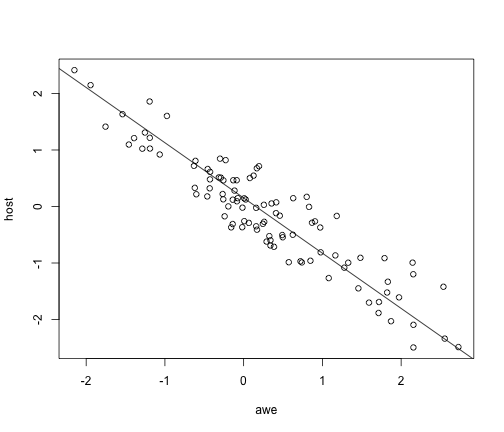
But PGLS is WAY more flexible than PICs. For example, we can include a discrete predictor:
pglsModel2 <- gls ( hostility ~ ecomorph , correlation = corBrownian ( phy = anoleTree ), data = anoleData , method = "ML" ) anova ( pglsModel2 ) ## Denom. DF: 93 ## numDF F-value p-value ## (Intercept) 1 0.01847 0.8922 ## ecomorph 6 0.21838 0.9700 ## (Intercept) ecomorphGB ecomorphT ecomorphTC ecomorphTG ecomorphTW ## 0.4844 -0.6316 -1.0585 -0.8558 -0.4086 -0.4039 ## ecomorphU ## -0.7022 We can even include multiple predictors:
pglsModel3 <- gls ( hostility ~ ecomorph * awesomeness , correlation = corBrownian ( phy = anoleTree ), data = anoleData , method = "ML" ) anova ( pglsModel3 ) ## Denom. DF: 86 ## numDF F-value p-value ## (Intercept) 1 0.1 0.7280 ## ecomorph 6 1.4 0.2090 ## awesomeness 1 472.9 <.0001 ## ecomorph:awesomeness 6 3.9 0.0017 We can also assume that the error structure follows an OU model rather than Brownian motion:
# Does not converge - and this is difficult to fix! pglsModelLambda <- gls ( hostility ~ awesomeness , correlation = corPagel ( 1 , phy = anoleTree , fixed = FALSE ), data = anoleData , method = "ML" ) ## Error: NA/NaN/Inf in foreign function call (arg 1) # this is a problem with scale. We can do a quick fix by making the branch # lengths longer. This will not affect the analysis other than rescaling a # nuisance parameter tempTree <- anoleTree tempTree $ edge.length <- tempTree $ edge.length * 100 pglsModelLambda <- gls ( hostility ~ awesomeness , correlation = corPagel ( 1 , phy = tempTree , fixed = FALSE ), data = anoleData , method = "ML" ) summary ( pglsModelLambda ) ## Generalized least squares fit by maximum likelihood ## Model: hostility ~ awesomeness ## Data: anoleData ## AIC BIC logLik ## 72.56 82.98 -32.28 ## ## Correlation Structure: corPagel ## Formula: ~1 ## Parameter estimate(s): ## lambda ## -0.1586 ## ## Coefficients: ## Value Std.Error t-value p-value ## (Intercept) 0.0612 0.01582 3.872 2e-04 ## awesomeness -0.8777 0.03104 -28.273 0e+00 ## ## Correlation: ## (Intr) ## awesomeness -1 ## ## Standardized residuals: ## Min Q1 Med Q3 Max ## -1.789463 -0.714775 0.003095 0.785093 2.232151 ## ## Residual standard error: 0.371 ## Degrees of freedom: 100 total; 98 residual pglsModelOU <- gls ( hostility ~ awesomeness , correlation = corMartins ( 1 , phy = tempTree ), data = anoleData , method = "ML" ) summary ( pglsModelOU ) ## Generalized least squares fit by maximum likelihood ## Model: hostility ~ awesomeness ## Data: anoleData ## AIC BIC logLik ## 96.63 107.1 -44.32 ## ## Correlation Structure: corMartins ## Formula: ~1 ## Parameter estimate(s): ## alpha ## 4.442 ## ## Coefficients: ## Value Std.Error t-value p-value ## (Intercept) 0.1084 0.03953 2.743 0.0072 ## awesomeness -0.8812 0.03658 -24.091 0.0000 ## ## Correlation: ## (Intr) ## awesomeness -0.269 ## ## Standardized residuals: ## Min Q1 Med Q3 Max ## -1.8665 -0.8133 -0.1104 0.6475 2.0919 ## ## Residual standard error: 0.3769 ## Degrees of freedom: 100 total; 98 residual Source: https://lukejharmon.github.io/ilhabela/instruction/2015/07/03/PGLS/
0 Response to "Pgls Between Discrete and Continuous Variables"
Enregistrer un commentaire